


Next: Statistics of a narrow
Up: High-order moments in the
Previous: High-order moments in the
Our starting point is the Zakharov equation (, ), which is
a deterministic nonlinear evolution equation for surface gravity waves in deep water.
Let's consider the potential flow of an ideal fluid of infinite depth.
Coordinates are chosen in such a way that the undisturbed surface of the
fluid coincides with the  plane.
The
plane.
The  -axis is pointed upward, and the acceleration of gravity
-axis is pointed upward, and the acceleration of gravity  is
pointed in the negative
is
pointed in the negative  -direction.
The surface elevation
-direction.
The surface elevation  may be written in
terms of a Fourier expansion as
may be written in
terms of a Fourier expansion as
![\begin{displaymath}
\eta = \int_{-\infty}^{\infty}{\rm d}\vec{k}
\left[ a(\vec{k})+a^*(-\vec{k}) \right]e^{i\vec{k}.\vec{x}},
\end{displaymath}](img5.png) |
(1) |
where
 and
and  is
the normal variable. Here,
is
the normal variable. Here,  is the wave number vector,
is the wave number vector,  is its
absolute value, and
is its
absolute value, and
 denotes the dispersion relation
of deep-water, gravity waves. Alternatively one may write for
denotes the dispersion relation
of deep-water, gravity waves. Alternatively one may write for 
 |
(2) |
where c.c denotes the complex conjugate.
() obtained from the Hamilton equations an
approximate evolution equation for the amplitude of the free surface
gravity waves, that contained the third order non-resonant and resonant
four-wave interactions.
In order to eliminate the effects of bound waves he applied on  a
canonical transformation of the type
a
canonical transformation of the type
 |
(3) |
where  is the normal variable of the free gravity waves. The evolution
equation for
is the normal variable of the free gravity waves. The evolution
equation for  , called the Zakharov equation, becomes
, called the Zakharov equation, becomes
 |
(4) |
where, for brevity we have introduced the notation
 , etc,
and the nonlinear transfer function
, etc,
and the nonlinear transfer function  as found by () enjoys a number of symmetries which guarantee that the
Zakharov equation is Hamiltonian and conserves wave energy.
In () it was shown that in the context of the
deep-water version of the Zakharov equation extreme surface gravity
waves are generated by nonlinear focusing in a random wave field.
This process also
causes the Benjamin-Feir instability of a uniform wave train.
As a consequence, for deep-water waves a considerable enhancement of
the probability for extreme waves is found. However, when going to shallow
waters, the effect of nonlinear focusing is greatly reduced. In fact
for a narrow band wave train (, ) it can be shown that the
nonlinear transfer coefficient
as found by () enjoys a number of symmetries which guarantee that the
Zakharov equation is Hamiltonian and conserves wave energy.
In () it was shown that in the context of the
deep-water version of the Zakharov equation extreme surface gravity
waves are generated by nonlinear focusing in a random wave field.
This process also
causes the Benjamin-Feir instability of a uniform wave train.
As a consequence, for deep-water waves a considerable enhancement of
the probability for extreme waves is found. However, when going to shallow
waters, the effect of nonlinear focusing is greatly reduced. In fact
for a narrow band wave train (, ) it can be shown that the
nonlinear transfer coefficient  vanishes when the dimensionless
water depth
vanishes when the dimensionless
water depth  . For smaller dimensionless depth nonlinear
effects will lead to defocusing and, consequently a considerable
reduction of extreme events. In this paper we only concentrate on the
deep-water case by restricting ourselves to
. For smaller dimensionless depth nonlinear
effects will lead to defocusing and, consequently a considerable
reduction of extreme events. In this paper we only concentrate on the
deep-water case by restricting ourselves to 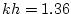 .
.
Thus, the nonlinear term in Eqn.(![[*]](crossref.png) ) will generate deviations from
the normal, Gaussian probability distribution function (PDF) for the
surface elevation. It is of interest to determine these deviations because
it gives us information on the occurrence of extreme sea states. However,
because the nonlinearity is of third order in amplitude, the skewness
of the free waves vanishes, while the fourth cumulant is finite.
On the other hand, the bound waves contribute to both the skewness and
the kurtosis of surface elevation PDF. In order to determine the effects
of the bound waves on the PDF of a random, nonlinear wave field one needs
to utilize the canonical transformation Eq.(
) will generate deviations from
the normal, Gaussian probability distribution function (PDF) for the
surface elevation. It is of interest to determine these deviations because
it gives us information on the occurrence of extreme sea states. However,
because the nonlinearity is of third order in amplitude, the skewness
of the free waves vanishes, while the fourth cumulant is finite.
On the other hand, the bound waves contribute to both the skewness and
the kurtosis of surface elevation PDF. In order to determine the effects
of the bound waves on the PDF of a random, nonlinear wave field one needs
to utilize the canonical transformation Eq.(![[*]](crossref.png) ). This results in
complicated expressions for skewness and kurtosis because one has to go
to third order in amplitude. The problem simplifies considerably when
the narrow-band approximation is adopted, because than one can simply
use the Stokes solution for the surface elevation. For example, in the
narrow-band approximation it is easy to show (see $ 2.2) that for a `typical'
steepness of the order
). This results in
complicated expressions for skewness and kurtosis because one has to go
to third order in amplitude. The problem simplifies considerably when
the narrow-band approximation is adopted, because than one can simply
use the Stokes solution for the surface elevation. For example, in the
narrow-band approximation it is easy to show (see $ 2.2) that for a `typical'
steepness of the order  bound waves contribute less than
bound waves contribute less than  to
the value of the kurtosis, so we can safely ignore their contribution.
to
the value of the kurtosis, so we can safely ignore their contribution.
Here, we are interested in obtaining the high-order moments of the surface
elevation for a homogeneous random sea. The homogeneity and stationarity
conditions imply
 |
(5) |
where we have introduced the usual action density  and the angle
brackets denote an ensemble average. As for narrow-band spectra bound
waves only have a small effect on the statistics of the surface
gravity waves we have to good approximation
and the angle
brackets denote an ensemble average. As for narrow-band spectra bound
waves only have a small effect on the statistics of the surface
gravity waves we have to good approximation
 |
|
|
(6) |
Envelope  and phase
and phase  are now defined as
are now defined as
 |
(7) |
hence,
 |
(8) |
where for a narrow-band wave train  and
and  are slowly varying
functions in time and space.
Now introduce the auxiliary variable
are slowly varying
functions in time and space.
Now introduce the auxiliary variable  in such a way that the
random variables
in such a way that the
random variables  and
and  are not correlated in the linear
wave field,
are not correlated in the linear
wave field,
 .
Thus,
.
Thus,
 |
(9) |
or,
 |
(10) |
Assuming zero mean for  , the second order moment
, the second order moment  is given by
is given by
 |
(11) |
According to Eq.(29) of Janssen (2003), the fourth moment
 and
kurtosis
and
kurtosis  can be obtained in terms of the action density
can be obtained in terms of the action density  and of the nonlinear transfer function
and of the nonlinear transfer function  . The result is
. The result is
where  is the fourth order cumulant of the surface
elevation
is the fourth order cumulant of the surface
elevation  and is equivalent to
and is equivalent to  , where
, where  is the
normalized fourth order moment, kurtosis of the surface elevation.
The transfer function
is the
normalized fourth order moment, kurtosis of the surface elevation.
The transfer function
 for large time t, where
for large time t, where
 and
and  denotes the principle value of the integral to avoid singularity in the
integral.
denotes the principle value of the integral to avoid singularity in the
integral.
For the cross-correlation between  and
and  ,
using Eq.(
,
using Eq.(![[*]](crossref.png) ) it immediately follows that
for homogeneous ocean waves indeed there is no correlation between
) it immediately follows that
for homogeneous ocean waves indeed there is no correlation between
 and
and  .
Then,
.
Then,
 |
(15) |
Using the second equation of (![[*]](crossref.png) ) this becomes
) this becomes
![$\displaystyle \langle \eta \; \zeta \rangle = -i \int_{-\infty}^{\infty}
{\rm d...
...{x}}+ \langle a_2a^*_1 \rangle
e^{i(\vec{k}_2-\vec{k}_1).\vec{x}} \right] = 0 !$](img49.png) |
|
|
(16) |
which vanishes because of the first equation of (![[*]](crossref.png) ).
The second cumulant we need is termed
).
The second cumulant we need is termed  and is defined as
and is defined as
 |
|
|
(17) |
where it is noted that
 .
Evaluating the RHS of (
.
Evaluating the RHS of (![[*]](crossref.png) ) using the definitions of
) using the definitions of  and
and
 one finds
one finds
 |
|
|
(18) |
hence  is, as expected, precisely three times smaller as
is, as expected, precisely three times smaller as
 .
.



Next: Statistics of a narrow
Up: High-order moments in the
Previous: High-order moments in the
2006-08-21
![]() plane.
The
plane.
The ![]() -axis is pointed upward, and the acceleration of gravity
-axis is pointed upward, and the acceleration of gravity ![]() is
pointed in the negative
is
pointed in the negative ![]() -direction.
The surface elevation
-direction.
The surface elevation ![]() may be written in
terms of a Fourier expansion as
may be written in
terms of a Fourier expansion as
![]() a
canonical transformation of the type
a
canonical transformation of the type
![[*]](crossref.png) ) will generate deviations from
the normal, Gaussian probability distribution function (PDF) for the
surface elevation. It is of interest to determine these deviations because
it gives us information on the occurrence of extreme sea states. However,
because the nonlinearity is of third order in amplitude, the skewness
of the free waves vanishes, while the fourth cumulant is finite.
On the other hand, the bound waves contribute to both the skewness and
the kurtosis of surface elevation PDF. In order to determine the effects
of the bound waves on the PDF of a random, nonlinear wave field one needs
to utilize the canonical transformation Eq.(
) will generate deviations from
the normal, Gaussian probability distribution function (PDF) for the
surface elevation. It is of interest to determine these deviations because
it gives us information on the occurrence of extreme sea states. However,
because the nonlinearity is of third order in amplitude, the skewness
of the free waves vanishes, while the fourth cumulant is finite.
On the other hand, the bound waves contribute to both the skewness and
the kurtosis of surface elevation PDF. In order to determine the effects
of the bound waves on the PDF of a random, nonlinear wave field one needs
to utilize the canonical transformation Eq.(![[*]](crossref.png) ). This results in
complicated expressions for skewness and kurtosis because one has to go
to third order in amplitude. The problem simplifies considerably when
the narrow-band approximation is adopted, because than one can simply
use the Stokes solution for the surface elevation. For example, in the
narrow-band approximation it is easy to show (see $ 2.2) that for a `typical'
steepness of the order
). This results in
complicated expressions for skewness and kurtosis because one has to go
to third order in amplitude. The problem simplifies considerably when
the narrow-band approximation is adopted, because than one can simply
use the Stokes solution for the surface elevation. For example, in the
narrow-band approximation it is easy to show (see $ 2.2) that for a `typical'
steepness of the order ![]() bound waves contribute less than
bound waves contribute less than ![]() to
the value of the kurtosis, so we can safely ignore their contribution.
to
the value of the kurtosis, so we can safely ignore their contribution.
![]() , the second order moment
, the second order moment ![]() is given by
is given by
![]() and
and ![]() ,
using Eq.(
,
using Eq.(![[*]](crossref.png) ) it immediately follows that
for homogeneous ocean waves indeed there is no correlation between
) it immediately follows that
for homogeneous ocean waves indeed there is no correlation between
![]() and
and ![]() .
Then,
.
Then,
![[*]](crossref.png) ) this becomes
) this becomes
![[*]](crossref.png) ).
The second cumulant we need is termed
).
The second cumulant we need is termed ![[*]](crossref.png) ) using the definitions of
) using the definitions of