Distribution of Wave Height

We assume that waves to be analyzed here are unidirectional with narrow banded spectra and satisfy the stationary and ergodic hypothesis. Let $\eta(t)$ be the sea surface elevation as a function of time $t$ and $\zeta(t)$ be its Hilbert transform. Assuming both $\eta(t)$ and $\zeta(t)$ are real zero-mean function with variance $\sigma$, we have

$$Z(t) = \eta(t) + i\zeta(t) = A(t)e^{i\phi(t)},$$ (1)

$$A(t) = \sqrt{\eta^2(t) + \zeta^2(t)},$$ (2)

$$\phi(t) = \tan^{-1}\left(\frac{\zeta(t)}{\eta(t)}\right).$$ (3)

Mori and Yasuda (2002b) investigated the wave height distribution as a function of kurtosis and skewness using the joint probability density function of $\eta(t)$ and $\zeta(t)$ for a narrow banded weakly nonlinear wave train semi-empirically.

$$p(H')\,dH' = \frac{H'}{4} \exp\left(-\frac{H'^2}{8}\right) \left[ 1 + \sum_{i,j}\beta_{i,j}B_{i,j}(H') \right]\,dH',$$ (4)

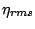where $H'$ is the wave height $H$ normalized by the root-mean-square of the surface elevation $\eta _{rms}$ and prime ' is dropped for simplicity hereafter. $\beta_{i,j}$ are coefficients containing the skewness and kurtosis of the water surface elevation $\eta(t)$,

$$\left. \begin{array}{l@{\, = \,}l} \beta_{4,1} & \displays... ...5\over 2^{28}\times 3^{4}}\,\mu_3^4 \\ \end{array}\right\},$$ (5)

and $B_{ij}$ are polynomials for $H$ (see Appendix).

The exceedance probability of wave heights is given by integrating Eq.(4) over the range of $[H,\infty)$:

$$P(H)=\exp\left(-\frac{H^2}{8}\right) \!\left[ 1 + \sum_{i,j}\beta_{i,j}E_{i,j}(H)\right]\!,$$ (6)

where $E_{i,j}(H)$ are polynomials for $H$ (see Appendix). Eq.(4) and (6) are the wave height and the exceedance wave height distributions of the nonlinear wave field in a unidirectional wave trains. This is a starting point of this paper.