

Next: Void Fraction and Turbulence
Up: RESULTS AND DISCUSSIONS
Previous: RESULTS AND DISCUSSIONS
The characteristics of entrained air in the surf zone will be examined in this section.
First, the horizontal (onshore-offshore) distributions of time-averaged void fraction
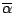 for Case 1 and 2 are shown in Figure 9.
The solid line indicates the void fraction for the mid-scale experiments and
dotted line indicates the void fraction for the large scale, respectively.
The maximum values of
for Case 1 and 2 are shown in Figure 9.
The solid line indicates the void fraction for the mid-scale experiments and
dotted line indicates the void fraction for the large scale, respectively.
The maximum values of
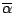 are 0.19 for Case 1 and 0.24 for
Case 2.
The maximum value decreases rapidly as the measurement location moves down to the still water level.
The difference of the maximum
are 0.19 for Case 1 and 0.24 for
Case 2.
The maximum value decreases rapidly as the measurement location moves down to the still water level.
The difference of the maximum
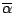 between
between  and 0.0 are four times for Case 1 and ten times for Case 2.
Cox and Shin (2003) reported exponential decay of the void fraction in time.
Therefore, it should be noted that the instantaneous void fraction is several times larger than time-averaged value.
The locations of
and 0.0 are four times for Case 1 and ten times for Case 2.
Cox and Shin (2003) reported exponential decay of the void fraction in time.
Therefore, it should be noted that the instantaneous void fraction is several times larger than time-averaged value.
The locations of
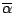 's peak for each vertical layer are about
's peak for each vertical layer are about  and
and  from the B.P. for Case 1 and 2, respectively.
For the spilling breaker (Case 1), the difference of
from the B.P. for Case 1 and 2, respectively.
For the spilling breaker (Case 1), the difference of
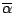 between
the mid- and small-scale experiments is about two times at most.
Moreover, for spilling/plunging breaker (Case 2), the difference of
between
the mid- and small-scale experiments is about two times at most.
Moreover, for spilling/plunging breaker (Case 2), the difference of
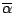 between the mid- and small-scale experiments is larger
than spilling case and becomes four times more at most.
This is because the strong wave breaking entraps a larger volume of air
and this large-size bulk of air can rise faster than a small one.
In addition, there is the second peak of void fraction in Case 2 of the mid-scale
experiments.
This is due to the second splash of breaking wave in the mid-scale
experiments but was not clearly observed in the small-scale experiments.
The relative size of the surf zone between the small and mid-scale
experiments were 0.53 in Case 1 and were 0.70 were Case 2.
These were not followed Froude similarity law.
Therefore, the scale effects of the void fraction on Case 2 is stronger than that of Case 1.
between the mid- and small-scale experiments is larger
than spilling case and becomes four times more at most.
This is because the strong wave breaking entraps a larger volume of air
and this large-size bulk of air can rise faster than a small one.
In addition, there is the second peak of void fraction in Case 2 of the mid-scale
experiments.
This is due to the second splash of breaking wave in the mid-scale
experiments but was not clearly observed in the small-scale experiments.
The relative size of the surf zone between the small and mid-scale
experiments were 0.53 in Case 1 and were 0.70 were Case 2.
These were not followed Froude similarity law.
Therefore, the scale effects of the void fraction on Case 2 is stronger than that of Case 1.
Figure 9:
Horizontal variations of time-averaged void fraction
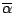 (solid line: mid-scale experiments, dotted line:
small-scale experiments).
(a) Case 1. (b) Case 2
(solid line: mid-scale experiments, dotted line:
small-scale experiments).
(a) Case 1. (b) Case 2
|
|
The scale effects on void fraction are significant in comparison with
two different scale experiments.
Entrapped air by breaking waves is split into small bubbles due to
the shear and turbulence of surrounding flows.
The early work of this problem for the general condition had been discussed by
Kolmogorov (1949) and Hinze (1955) in the middle of the last
century and a large bibliography has been generated (i.e. Martínez-Bazán
et al., 1999).
Therefore, it is of interest to verify the influence of the void fraction on
the bubble size spectra.
The spatial changes of bubble size spectra for large scale bubbles
(chord length  mm) above the still water level are shown in Figure 10.
The horizontal axes are bubble size
mm) above the still water level are shown in Figure 10.
The horizontal axes are bubble size 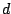 (chord length) and normalized
distance from the breaking point
(chord length) and normalized
distance from the breaking point  , respectively, and the
vertical axis
, respectively, and the
vertical axis  is the number of bubbles per unit square per one wave period.
The left hand side and right hand side in Figure 10 are the spatial
variation of the measured bubble size
is the number of bubbles per unit square per one wave period.
The left hand side and right hand side in Figure 10 are the spatial
variation of the measured bubble size 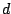 for the mid- and small-scale experiments, respectively.
The bubble size spectra increase rapidly from the B.P. in Case 1 of the mid-scale experiments.
After that, the number of small size bubbles decreases monotonically
towards the shoreline, although the time-averaged void fraction remains constant as shown in Figure 9 (a).
The difference between Case 1 and 2 of the mid-scale experiment is clear.
The bubble size spectra in Case 2 of the mid-scale experiment show two clear peaks spatially, and the locations of peaks appear at the same location of the time-averaged void fraction as shown in Figure 9 (b).
The difference of the spatial distribution of bubble size spectra
between Case 1 and Case 2 of the mid-scale experiment is hard to explain but advection effect is one possibility.
There is no clear peak and the continuous shape of the spectra can
be observed in the small-scale experiments due to statistical fluctuation.
Thus, the power-law scaling of bubble size spectra is discussed next paragraph.
for the mid- and small-scale experiments, respectively.
The bubble size spectra increase rapidly from the B.P. in Case 1 of the mid-scale experiments.
After that, the number of small size bubbles decreases monotonically
towards the shoreline, although the time-averaged void fraction remains constant as shown in Figure 9 (a).
The difference between Case 1 and 2 of the mid-scale experiment is clear.
The bubble size spectra in Case 2 of the mid-scale experiment show two clear peaks spatially, and the locations of peaks appear at the same location of the time-averaged void fraction as shown in Figure 9 (b).
The difference of the spatial distribution of bubble size spectra
between Case 1 and Case 2 of the mid-scale experiment is hard to explain but advection effect is one possibility.
There is no clear peak and the continuous shape of the spectra can
be observed in the small-scale experiments due to statistical fluctuation.
Thus, the power-law scaling of bubble size spectra is discussed next paragraph.
Figure 10:
Horizontal variations of bubble chord length spectra at 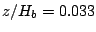 (horizontal axes: distance from B.P. and bubble size, vertical axis:
number of bubble per one wave period).
(a) Case 1 (left panel: mid-scale experiments, right panel: small-scale
experiments).
(b) Case 2 (ditto).
(horizontal axes: distance from B.P. and bubble size, vertical axis:
number of bubble per one wave period).
(a) Case 1 (left panel: mid-scale experiments, right panel: small-scale
experiments).
(b) Case 2 (ditto).
|
|
To check the power-law scaling of the bubble size spectra,
Figure 11 shows the PDF of time-space averaged bubble size from top to
bottom and offshore to onshore side.
 |
(6) |
where  is the PDF,
is the PDF,  is total number of measured bubble per one
wave period and
is total number of measured bubble per one
wave period and  is the increment of the bubble chord length of bubble
size spectra.
The spectra are normalized by the total number of bubbles for each case.
Therefore the number of bubbles are ignored in the figure.
The notations of
is the increment of the bubble chord length of bubble
size spectra.
The spectra are normalized by the total number of bubbles for each case.
Therefore the number of bubbles are ignored in the figure.
The notations of 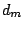 in the figure indicate the mean chord
length, and the power-law scaling of bubble size
in the figure indicate the mean chord
length, and the power-law scaling of bubble size 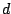 and linear lines are given power-law curves.
The power-law of the bubble size spectrum tail was estimated by the least square method in a log-scale domain.
The mean chord lengths for mid- and small-scale experiments are 0.56 cm
and 0.51 cm in Case 1 and 0.56 cm and 0.61 cm in Case 2, respectively.
Thus, there is no influence of scale and breaker type on the mean chord length.
On the other hand, the power-law scalings are also similar to each case
and the different experimental scales.
The power-law scalings are in between
and linear lines are given power-law curves.
The power-law of the bubble size spectrum tail was estimated by the least square method in a log-scale domain.
The mean chord lengths for mid- and small-scale experiments are 0.56 cm
and 0.51 cm in Case 1 and 0.56 cm and 0.61 cm in Case 2, respectively.
Thus, there is no influence of scale and breaker type on the mean chord length.
On the other hand, the power-law scalings are also similar to each case
and the different experimental scales.
The power-law scalings are in between
 .
The Weber number
.
The Weber number  can be defined as
can be defined as
 |
(7) |
where  is the water density,
is the water density,  is the surface tension
coefficient,
is the surface tension
coefficient,  is the bubble diameter, and
is the bubble diameter, and 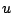 is turbulence velocity
of the bubble scale
is turbulence velocity
of the bubble scale  .
The turbulence velocity
.
The turbulence velocity 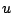 of the bubble scale in the
inertial range can be given by
of the bubble scale in the
inertial range can be given by
 where
where
 is the energy dissipation rate.
Then, the Hinze scale
is the energy dissipation rate.
Then, the Hinze scale  (Deane and Stokes, 2002) of bubble splitting can be given by
(Deane and Stokes, 2002) of bubble splitting can be given by
 |
(8) |
where
 and
and  the critical Weber number.
Garrett et al. (2000) proposed semi-empirical
the critical Weber number.
Garrett et al. (2000) proposed semi-empirical  power-law scaling for
the bubble which is larger than the Hinze scale based on the
discussion of bubble fragmentation in the strong turbulence flow below the trough level.
The measured power-law scaling of bubble size spectra is wider than
Garrett et al. (2000).
On the other hand, Deane and Stokes (2002) measured a
power-law scaling for
the bubble which is larger than the Hinze scale based on the
discussion of bubble fragmentation in the strong turbulence flow below the trough level.
The measured power-law scaling of bubble size spectra is wider than
Garrett et al. (2000).
On the other hand, Deane and Stokes (2002) measured a  power-law
scaling, smaller than the Hinze scale (1mm) of the acoustically active phase near
the crest.
The power-law scaling of the time-averaged chord length shown in
Figure 11 is similar to the power-law scaling of the small-scale bubble of
Deane and Stokes (2002).
Although we measured the bubble chord length, the theory is formulated
for the bubble diameter.
Therefore, the power-law of the spectra of DVP measured chord length can be
changed into bubble diameter spectra as discussed in a previous section.
Therefore, the estimation of the Hinze scale is important to discuss in detail.
Following Hinze (1995),
power-law
scaling, smaller than the Hinze scale (1mm) of the acoustically active phase near
the crest.
The power-law scaling of the time-averaged chord length shown in
Figure 11 is similar to the power-law scaling of the small-scale bubble of
Deane and Stokes (2002).
Although we measured the bubble chord length, the theory is formulated
for the bubble diameter.
Therefore, the power-law of the spectra of DVP measured chord length can be
changed into bubble diameter spectra as discussed in a previous section.
Therefore, the estimation of the Hinze scale is important to discuss in detail.
Following Hinze (1995),  if
if  is defined such that 95% of
the air is contained in bubbles with a radius less than
is defined such that 95% of
the air is contained in bubbles with a radius less than  .
Battjes and Janssen (1978) formulated the depth-averaged energy
dissipation rate
.
Battjes and Janssen (1978) formulated the depth-averaged energy
dissipation rate
 for surf zone breaking waves as
for surf zone breaking waves as
 |
(9) |
where  is the water depth.
Similar formulations have also been made by the other researcher with
different coefficient and parameters (e.g. Feddersen and Trowbridge, 2005).
For the mid-scale and small-scale experiments of Case 1,
is the water depth.
Similar formulations have also been made by the other researcher with
different coefficient and parameters (e.g. Feddersen and Trowbridge, 2005).
For the mid-scale and small-scale experiments of Case 1,
 are
0.254 and 0.0414 W/kg by Battjes and Janssen theory and it gives
are
0.254 and 0.0414 W/kg by Battjes and Janssen theory and it gives
 and 4.28 mm, respectively.
However, the energy dissipation rate shows a dependence on water depth
(e.g. Ting and Kirby, 1996).
Svendsen (1987) modeled the dissipation rate through the relation
and 4.28 mm, respectively.
However, the energy dissipation rate shows a dependence on water depth
(e.g. Ting and Kirby, 1996).
Svendsen (1987) modeled the dissipation rate through the relation
 |
(10) |
where  is the empirical constant and
is the empirical constant and  is the length scale, using
is the length scale, using  for the spilling breaker.
The measured
for the spilling breaker.
The measured  was
was
 which will be shown
later, and it gives a dissipation rate of
which will be shown
later, and it gives a dissipation rate of
 W/kg.
Similar experiments on 1/35 plain slope was conducted by Ting and Kirby (1996).
Their breaking wave height
W/kg.
Similar experiments on 1/35 plain slope was conducted by Ting and Kirby (1996).
Their breaking wave height 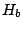 was 0.163 m and is almost equivalent to
our Case 1, although their water depth was different.
The maximum energy dissipation measured by Ting and Kirby (1996) was 0.01 W/kg
below the trough level.
Therefore, the measured or estimated energy dissipation above still
water level is ten times larger than below the trough level.
If the bubble chord length can be approximated by bubble diameter,
the experimental data of the mid-scale and small-scale experiments shows
similar chord length spectrum profiles with different peak chord length.
The scale differences in this study only play peak chord length difference
with the same profile of size distribution.
The detail mechanisms and relationship between the Hinze scale and
energy dissipation should keep for future study.
was 0.163 m and is almost equivalent to
our Case 1, although their water depth was different.
The maximum energy dissipation measured by Ting and Kirby (1996) was 0.01 W/kg
below the trough level.
Therefore, the measured or estimated energy dissipation above still
water level is ten times larger than below the trough level.
If the bubble chord length can be approximated by bubble diameter,
the experimental data of the mid-scale and small-scale experiments shows
similar chord length spectrum profiles with different peak chord length.
The scale differences in this study only play peak chord length difference
with the same profile of size distribution.
The detail mechanisms and relationship between the Hinze scale and
energy dissipation should keep for future study.
Figure 11:
PDF of time-space averaged bubble chord length and their statistics
(dashed line and  : mid-scale experiments, dotted line and
: mid-scale experiments, dotted line and
 : small-scale experiments).
(a) Case 1 (left: linear scale, right: log scale).
(b) Case 2 (ditto).
: small-scale experiments).
(a) Case 1 (left: linear scale, right: log scale).
(b) Case 2 (ditto).
|
|


Next: Void Fraction and Turbulence
Up: RESULTS AND DISCUSSIONS
Previous: RESULTS AND DISCUSSIONS
2006-12-14
![]() for Case 1 and 2 are shown in Figure 9.
The solid line indicates the void fraction for the mid-scale experiments and
dotted line indicates the void fraction for the large scale, respectively.
The maximum values of
for Case 1 and 2 are shown in Figure 9.
The solid line indicates the void fraction for the mid-scale experiments and
dotted line indicates the void fraction for the large scale, respectively.
The maximum values of
![]() are 0.19 for Case 1 and 0.24 for
Case 2.
The maximum value decreases rapidly as the measurement location moves down to the still water level.
The difference of the maximum
are 0.19 for Case 1 and 0.24 for
Case 2.
The maximum value decreases rapidly as the measurement location moves down to the still water level.
The difference of the maximum
![]() between
between ![]() and 0.0 are four times for Case 1 and ten times for Case 2.
Cox and Shin (2003) reported exponential decay of the void fraction in time.
Therefore, it should be noted that the instantaneous void fraction is several times larger than time-averaged value.
The locations of
and 0.0 are four times for Case 1 and ten times for Case 2.
Cox and Shin (2003) reported exponential decay of the void fraction in time.
Therefore, it should be noted that the instantaneous void fraction is several times larger than time-averaged value.
The locations of
![]() 's peak for each vertical layer are about
's peak for each vertical layer are about ![]() and
and ![]() from the B.P. for Case 1 and 2, respectively.
For the spilling breaker (Case 1), the difference of
from the B.P. for Case 1 and 2, respectively.
For the spilling breaker (Case 1), the difference of
![]() between
the mid- and small-scale experiments is about two times at most.
Moreover, for spilling/plunging breaker (Case 2), the difference of
between
the mid- and small-scale experiments is about two times at most.
Moreover, for spilling/plunging breaker (Case 2), the difference of
![]() between the mid- and small-scale experiments is larger
than spilling case and becomes four times more at most.
This is because the strong wave breaking entraps a larger volume of air
and this large-size bulk of air can rise faster than a small one.
In addition, there is the second peak of void fraction in Case 2 of the mid-scale
experiments.
This is due to the second splash of breaking wave in the mid-scale
experiments but was not clearly observed in the small-scale experiments.
The relative size of the surf zone between the small and mid-scale
experiments were 0.53 in Case 1 and were 0.70 were Case 2.
These were not followed Froude similarity law.
Therefore, the scale effects of the void fraction on Case 2 is stronger than that of Case 1.
between the mid- and small-scale experiments is larger
than spilling case and becomes four times more at most.
This is because the strong wave breaking entraps a larger volume of air
and this large-size bulk of air can rise faster than a small one.
In addition, there is the second peak of void fraction in Case 2 of the mid-scale
experiments.
This is due to the second splash of breaking wave in the mid-scale
experiments but was not clearly observed in the small-scale experiments.
The relative size of the surf zone between the small and mid-scale
experiments were 0.53 in Case 1 and were 0.70 were Case 2.
These were not followed Froude similarity law.
Therefore, the scale effects of the void fraction on Case 2 is stronger than that of Case 1.
![\includegraphics[width=10.0 cm]{figures/fig09.eps}](img74.png)
![]() mm) above the still water level are shown in Figure 10.
The horizontal axes are bubble size
mm) above the still water level are shown in Figure 10.
The horizontal axes are bubble size ![]() (chord length) and normalized
distance from the breaking point
(chord length) and normalized
distance from the breaking point ![]() , respectively, and the
vertical axis
, respectively, and the
vertical axis ![]() is the number of bubbles per unit square per one wave period.
The left hand side and right hand side in Figure 10 are the spatial
variation of the measured bubble size
is the number of bubbles per unit square per one wave period.
The left hand side and right hand side in Figure 10 are the spatial
variation of the measured bubble size ![]() for the mid- and small-scale experiments, respectively.
The bubble size spectra increase rapidly from the B.P. in Case 1 of the mid-scale experiments.
After that, the number of small size bubbles decreases monotonically
towards the shoreline, although the time-averaged void fraction remains constant as shown in Figure 9 (a).
The difference between Case 1 and 2 of the mid-scale experiment is clear.
The bubble size spectra in Case 2 of the mid-scale experiment show two clear peaks spatially, and the locations of peaks appear at the same location of the time-averaged void fraction as shown in Figure 9 (b).
The difference of the spatial distribution of bubble size spectra
between Case 1 and Case 2 of the mid-scale experiment is hard to explain but advection effect is one possibility.
There is no clear peak and the continuous shape of the spectra can
be observed in the small-scale experiments due to statistical fluctuation.
Thus, the power-law scaling of bubble size spectra is discussed next paragraph.
for the mid- and small-scale experiments, respectively.
The bubble size spectra increase rapidly from the B.P. in Case 1 of the mid-scale experiments.
After that, the number of small size bubbles decreases monotonically
towards the shoreline, although the time-averaged void fraction remains constant as shown in Figure 9 (a).
The difference between Case 1 and 2 of the mid-scale experiment is clear.
The bubble size spectra in Case 2 of the mid-scale experiment show two clear peaks spatially, and the locations of peaks appear at the same location of the time-averaged void fraction as shown in Figure 9 (b).
The difference of the spatial distribution of bubble size spectra
between Case 1 and Case 2 of the mid-scale experiment is hard to explain but advection effect is one possibility.
There is no clear peak and the continuous shape of the spectra can
be observed in the small-scale experiments due to statistical fluctuation.
Thus, the power-law scaling of bubble size spectra is discussed next paragraph.
![\includegraphics[width=14.5 cm]{figures/fig10.eps}](img78.png)
![\includegraphics[width=12.0 cm]{figures/fig11.eps}](img107.png)