

Next: CONCLUSIONS
Up: RESULTS AND DISCUSSIONS
Previous: Void Fraction and Bubble
The entrapped air induced by wave breaking generates strong turbulence
near the free surface.
Cox and Shin (2003) reported the dependence of void fraction on turbulent
intensity in the bore region of surf zone waves.
Therefore, the relationship between void fraction and turbulence is very
significant.
Moreover, it is also important for turbulence modeling.
The simultaneous observations of void fraction and turbulence for
the breaking waves of the mid-scale experiments were conducted in this study.
Therefore, the relationship between the void fraction and turbulence will be examined in this section.
Using the phase-averaged method the velocity data were divided
by the mean and turbulence components of the velocity.
Figure 12 shows an example of phase-averaged time series of surface
elevation and turbulence components at 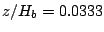 (above still water level) for Case 1.
The notation of
(above still water level) for Case 1.
The notation of 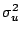 ,
, 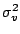 and
and 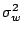 are
turbulent stress for velocity components
are
turbulent stress for velocity components 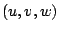 .
Similar to the laboratory experiments by
Ting and Kirby (1994), Cox et al. (1994) and Cox and Shin (2003).
They showed that the temporal variation of
.
Similar to the laboratory experiments by
Ting and Kirby (1994), Cox et al. (1994) and Cox and Shin (2003).
They showed that the temporal variation of 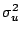 in the surf zone
fluctuated in the range
in the surf zone
fluctuated in the range
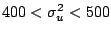
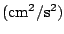 .
Figure 12 shows that the magnitude of
.
Figure 12 shows that the magnitude of 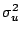 is similar at the
still water level
is similar at the
still water level 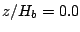 but is large above the still water level.
The peak of turbulent stress is located at the front of crest and decreases linearly as time passes.
This is a typical time series of turbulence characteristics of this and
other laboratory experiments on depth-limited breaking waves.
but is large above the still water level.
The peak of turbulent stress is located at the front of crest and decreases linearly as time passes.
This is a typical time series of turbulence characteristics of this and
other laboratory experiments on depth-limited breaking waves.
Figure:
Example of phase-averaged surface elevation
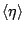 and turbulence
components 1.0m from B.P. in Case 1. (a) Free surface
and turbulence
components 1.0m from B.P. in Case 1. (a) Free surface 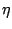 (solid) and standard deviation
(solid) and standard deviation
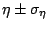 , (b)-(d) temporal variation of
, (b)-(d) temporal variation of 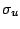 (thick solid),
(thick solid), 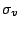 (thin solid) and
(thin solid) and 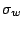 (dotted) and (e) the phase-averaged void fraction
(dotted) and (e) the phase-averaged void fraction
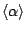
|
|
Figure 13 shows the horizontal relationship between time-averaged
void fraction:
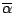 and time-averaged total kinetic energy (TKE):
and time-averaged total kinetic energy (TKE): 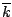 for Case 1-3.
The total kinetic energy and time-averaged TKE are defined by
for Case 1-3.
The total kinetic energy and time-averaged TKE are defined by
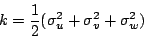 |
(11) |
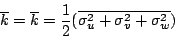 |
(12) |
The spatial variations of time-averaged void fraction
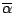 and
time-averaged TKE:
and
time-averaged TKE: 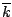 show similar tendency, although the peak of
show similar tendency, although the peak of
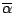 appears
appears
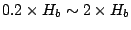 offshore than the peak of
offshore than the peak of 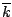 .
The short spatial lag between
.
The short spatial lag between
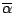 and
and 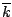 might be associated
with the entrapped air generated turbulence.
The spatial variations of the turbulence and void fraction are highly
correlated below
might be associated
with the entrapped air generated turbulence.
The spatial variations of the turbulence and void fraction are highly
correlated below 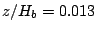 .
The entrained bulk of air and bubbles generate turbulence and turbulence
splits the coarse bubbles into fine bubbles in this phase.
Moreover, TKE and the void fraction increased ten times from
.
The entrained bulk of air and bubbles generate turbulence and turbulence
splits the coarse bubbles into fine bubbles in this phase.
Moreover, TKE and the void fraction increased ten times from
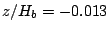 to
to 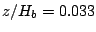 , thus two-phase flow characteristics is
remarkable near the wave crest.
In addition, there is significant difference between the turbulence and void fraction
, thus two-phase flow characteristics is
remarkable near the wave crest.
In addition, there is significant difference between the turbulence and void fraction 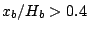 at
at 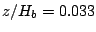 in Case 1.
The void fraction at
in Case 1.
The void fraction at 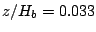 keeps high level after reached at its
peak but
keeps high level after reached at its
peak but 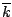 is decreased in this region.
This vertical level is re-aerated region of breaking wave induced bubble and is corresponds to silent-phase by Deane and Stokes classification.
Neglecting the short spatial lag between void fraction and TKE,
the direct comparison between time-averaged void fraction:
is decreased in this region.
This vertical level is re-aerated region of breaking wave induced bubble and is corresponds to silent-phase by Deane and Stokes classification.
Neglecting the short spatial lag between void fraction and TKE,
the direct comparison between time-averaged void fraction:
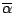 and normalized time-averaged TKE:
and normalized time-averaged TKE: 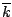 of the all measuring locations is shown in Figure 14.
For small value
of the all measuring locations is shown in Figure 14.
For small value
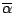 or
or 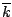 , the relationship between them
shows high correlation and it becomes scattered at high void fraction or TKE region.
Overall, the relationship between time-averaged void fraction and time-averaged TKE is clear.
In addition, the incident wave dependence on the relationship between
, the relationship between them
shows high correlation and it becomes scattered at high void fraction or TKE region.
Overall, the relationship between time-averaged void fraction and time-averaged TKE is clear.
In addition, the incident wave dependence on the relationship between
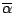 and
and 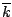 .
The similar analysis has been examined by Cox and Shin (2003) but their
results were more scattered than us.
This is based on the limitation of accurate turbulence measurements near
the wave crest.
The relation between the void fraction and TKE, the scale dependence of
void fraction and the further theoretical consideration will be required finding the universal relationship between the turbulence characteristics of breaking wave and void fraction.
.
The similar analysis has been examined by Cox and Shin (2003) but their
results were more scattered than us.
This is based on the limitation of accurate turbulence measurements near
the wave crest.
The relation between the void fraction and TKE, the scale dependence of
void fraction and the further theoretical consideration will be required finding the universal relationship between the turbulence characteristics of breaking wave and void fraction.
Figure 13:
Horizontal relationship between time-averaged void fraction
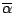 (solid line) and time-averaged TKE:
(solid line) and time-averaged TKE: 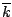 (dotted line) in Case 1
(dotted line) in Case 1
|
|
Figure 14:
Relationship between time-averaged TKE: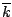 and time-averaged void fraction
and time-averaged void fraction
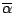 . (
. ( : Case 1,
: Case 1, 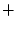 : Case 2,
: Case 2,  : Case 3)
: Case 3)
|
|


Next: CONCLUSIONS
Up: RESULTS AND DISCUSSIONS
Previous: Void Fraction and Bubble
2006-12-14
![]() (above still water level) for Case 1.
The notation of
(above still water level) for Case 1.
The notation of ![]() ,
, ![]() and
and ![]() are
turbulent stress for velocity components
are
turbulent stress for velocity components ![]() .
Similar to the laboratory experiments by
Ting and Kirby (1994), Cox et al. (1994) and Cox and Shin (2003).
They showed that the temporal variation of
.
Similar to the laboratory experiments by
Ting and Kirby (1994), Cox et al. (1994) and Cox and Shin (2003).
They showed that the temporal variation of ![]() in the surf zone
fluctuated in the range
in the surf zone
fluctuated in the range
![]()
![]() .
Figure 12 shows that the magnitude of
.
Figure 12 shows that the magnitude of ![]() is similar at the
still water level
is similar at the
still water level ![]() but is large above the still water level.
The peak of turbulent stress is located at the front of crest and decreases linearly as time passes.
This is a typical time series of turbulence characteristics of this and
other laboratory experiments on depth-limited breaking waves.
but is large above the still water level.
The peak of turbulent stress is located at the front of crest and decreases linearly as time passes.
This is a typical time series of turbulence characteristics of this and
other laboratory experiments on depth-limited breaking waves.
![\includegraphics[width=12.0 cm]{figures/fig12.eps}](img117.png)
![]() and time-averaged total kinetic energy (TKE):
and time-averaged total kinetic energy (TKE): ![]() for Case 1-3.
The total kinetic energy and time-averaged TKE are defined by
for Case 1-3.
The total kinetic energy and time-averaged TKE are defined by
![\includegraphics[width=12.0 cm]{figures/fig13.eps}](img126.png)
![\includegraphics[width=10.0 cm]{figures/fig14.eps}](img127.png)