


Next: Bibliography
Up: JPO_freakwave_html
Previous: Acknowledgements
Starting from Eq.(![[*]](crossref.png) ), we simplify the denominator in the integral
and we introduce the BF index. This gives for the kurtosis
), we simplify the denominator in the integral
and we introduce the BF index. This gives for the kurtosis
where
![$\displaystyle J={\cal P}\int_{-\infty}^{\infty}\frac{ {\rm d}\nu_1{\rm d}\nu_2{...
...}
\frac{e^{-\frac{1}{2}[\nu_1^2+\nu_2^2+\nu_3^2]}} {(\nu_3-\nu_1)(\nu_3-\nu_2)}$](img171.png) |
|
|
(54) |
Let us determine this integral, which, as will be seen, is not a trivial
exercise. Introduce
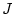 , hence,
, hence,
![$\displaystyle J=\frac{1}{2\pi^{3/2}}{\cal P}\int_{-\infty}^{\infty} {\rm d}t_1{\rm d}t_2{\rm d}t_3
\frac{e^{-[t_1^2+t_2^2+t_3^2]}} {(t_1-t_3)(t_2-t_3)}$](img173.png) |
|
|
(55) |
Performing the integration over 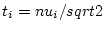 and
and 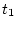 first, then
first, then
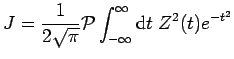 |
|
|
(56) |
where
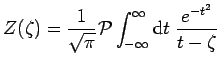 |
|
|
(57) |
is also called the Plasma Dispersion Function. It is customary to
express the function 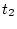 in terms of the error function with complex
argument. However, normally the Residu at
in terms of the error function with complex
argument. However, normally the Residu at 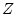 is included. It is
omitted here because only the Principal Value is required. Hence,
is included. It is
omitted here because only the Principal Value is required. Hence,
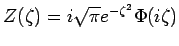 |
|
|
(58) |
where
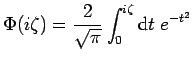 |
|
|
(59) |
is the error function (Note that in the usual Plasma dispersion function
an integration from 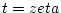 to
to 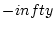 is added). Elimination of
is added). Elimination of 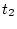 thus gives
for
thus gives
for 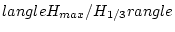
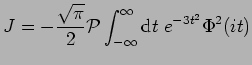 |
|
|
(60) |
We now evaluate 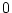
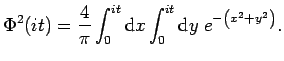 |
|
|
(61) |
We can perform one integration by introducing polar coordinates
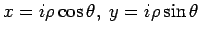 |
|
|
(62) |
and the result becomes
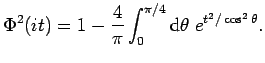 |
|
|
(63) |
Therefore,
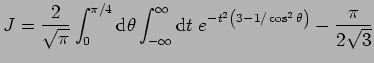 |
|
|
(64) |
Integration over  now gives
now gives
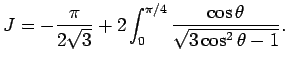 |
|
|
(65) |
The remaining integral can be evaluated by means of the transformation
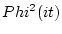 and equals
and equals 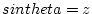 . The final result for
. The final result for
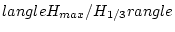 is
is
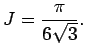 |
|
|
(66) |



Next: Bibliography
Up: JPO_freakwave_html
Previous: Acknowledgements
2006-08-21
![[*]](crossref.png) ), we simplify the denominator in the integral
and we introduce the BF index. This gives for the kurtosis
), we simplify the denominator in the integral
and we introduce the BF index. This gives for the kurtosis