


Next: Comparison of the theory
Up: Wave height distribution
Previous: Wave height distribution
In the previous section we have obtained for homogeneous random waves a
clear relationship between spectral shape and kurtosis through the resonant and
non-resonant four-wave interactions of the Zakharov equation.
Following a central limit theorem, linear, dispersive random waves have a
Gaussian PDF for the surface elevation. Finite amplitude effects result,
however, in deviations from the Normal distribution, as measured by a finite
skewness and kurtosis.
() investigated the influence of second-order
nonlinearity on wave crest distributions.
However,for narrow band wave trains it will be shown that the wave
height distribution only depends on the kurtosis.
Therefore, we shall formulate the
relationship between wave height distribution and kurtosis to examine
analytically the effects of kurtosis on freak wave occurrence.
We assume that waves to be analyzed here are unidirectional with
narrow banded spectra and satisfy the stationary and ergodic hypothesis.
Let  be the sea surface elevation as a function of time
be the sea surface elevation as a function of time  and
and
 an auxiliary variable such that
an auxiliary variable such that  and
and  are not correlated.
Assuming both
are not correlated.
Assuming both  and
and  are real zero-mean function with variance
are real zero-mean function with variance  , we have
, we have
where  is the envelope of the wave train and
is the envelope of the wave train and  the phase.
() investigated the wave height distribution as a function
of kurtosis and skewness using the joint probability density function of
the phase.
() investigated the wave height distribution as a function
of kurtosis and skewness using the joint probability density function of
 and
and  for a narrow banded weakly nonlinear wave train.
We will follow this approach closely.
For weakly nonlinear waves deviations from the Normal distribution are
small. In those circumstances the PDF of the surface elevation
can be described by the Edgeworth distribution. As there is no-correlation
between
for a narrow banded weakly nonlinear wave train.
We will follow this approach closely.
For weakly nonlinear waves deviations from the Normal distribution are
small. In those circumstances the PDF of the surface elevation
can be described by the Edgeworth distribution. As there is no-correlation
between  and
and  , the joint probability density function of
, the joint probability density function of
 and
and  becomes
becomes
where  is the
is the  th order Hermite polynomial
th order Hermite polynomial
 |
|
|
(39) |
All variables will be normalized by the variance of
the surface elevation
 (where
(where 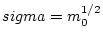 is the zero moment
of the wave spectrum) and have zero-mean.
is the zero moment
of the wave spectrum) and have zero-mean.
Keeping (![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) ) in mind, the PDF of the envelope
) in mind, the PDF of the envelope  follows now immediately from an integration of the joint probability
distribution
follows now immediately from an integration of the joint probability
distribution
 |
|
|
(40) |
over  , hence
, hence
 |
|
|
(41) |
Performing the integration over  it is found that the
first term of (
it is found that the
first term of (![[*]](crossref.png) ) gives the usual Rayleigh distribution
) gives the usual Rayleigh distribution
 , while the terms involving the skewness
, while the terms involving the skewness  ,
etc, all integrate to zero because they are odd functions of
,
etc, all integrate to zero because they are odd functions of  .
The third term does give contributions and as a result we find
.
The third term does give contributions and as a result we find
![$\displaystyle p(A)=A e^{-\frac{1}{2}A^2}
\left[1+\frac{1}{4}
\left(\kappa_{40} + \kappa_{22}\right)
\left(1-A^2+\frac{1}{8}A^4\right)
\right],$](img112.png) |
|
|
(42) |
where we have used
 , a relation that can easily
be verified. Finally, using
, a relation that can easily
be verified. Finally, using
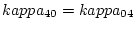 the final
result for the narrow-band approximation of the PDF of the envelope
becomes
the final
result for the narrow-band approximation of the PDF of the envelope
becomes
![$\displaystyle p(A)=A e^{-\frac{1}{2}A^2}
\left[
1 + \frac{1}{3}\kappa_{40}\left(1-A^2+\frac{1}{8}A^4\right)
\right].$](img115.png) |
|
|
(43) |
It is emphasized that, as expected, the PDF for the envelope does not
contain contributions that are linear in the skewness. However, as
follows from Eqns.(![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) ), the skewness is,
compared to the kurtosis, a large quantity. Quadratic terms in skewness
could give an equally important contribution to the PDF of
), the skewness is,
compared to the kurtosis, a large quantity. Quadratic terms in skewness
could give an equally important contribution to the PDF of  as the
kurtosis terms. This was pointed out by () and it required
to extend the Edgeworth distribution to sixth order. Nevertheless,
this additional term, proportional to
as the
kurtosis terms. This was pointed out by () and it required
to extend the Edgeworth distribution to sixth order. Nevertheless,
this additional term, proportional to  , gives for narrow-band wave
trains only a small contribution to the PDF for the same reason as the
bound wave contribution to the kurtosis may be neglected.
, gives for narrow-band wave
trains only a small contribution to the PDF for the same reason as the
bound wave contribution to the kurtosis may be neglected.
From the result (![[*]](crossref.png) ) interesting consequences for the distribution of
maximum wave heights may be derived. In the narrow band approximation
wave height
) interesting consequences for the distribution of
maximum wave heights may be derived. In the narrow band approximation
wave height 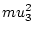 equals
equals 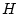 and hence the wave height PDF becomes
and hence the wave height PDF becomes
![$\displaystyle p(H)=\frac{1}{4}H e^{-\frac{1}{8}H^2}\left[1+\kappa_{40}A_H(H)\right],$](img119.png) |
|
|
(44) |
where
 |
|
|
(45) |
The exceedance probability  for wave height then follows from
an integration of (
for wave height then follows from
an integration of (![[*]](crossref.png) ) from
) from 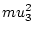 to
to  :
:
![$\displaystyle P_H(H)=e^{-\frac{1}{8}H^2}\left[1+\kappa_{40}B_H(H)\right],$](img123.png) |
|
|
(46) |
where
 |
|
|
(47) |



Next: Comparison of the theory
Up: Wave height distribution
Previous: Wave height distribution
2006-08-21
![]() be the sea surface elevation as a function of time
be the sea surface elevation as a function of time ![]() and
and
![]() an auxiliary variable such that
an auxiliary variable such that ![]() and
and ![]() are not correlated.
Assuming both
are not correlated.
Assuming both ![]() and
and ![]() are real zero-mean function with variance
are real zero-mean function with variance ![]() , we have
, we have
![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) ) in mind, the PDF of the envelope
) in mind, the PDF of the envelope ![]() follows now immediately from an integration of the joint probability
distribution
follows now immediately from an integration of the joint probability
distribution
![[*]](crossref.png) ) gives the usual Rayleigh distribution
) gives the usual Rayleigh distribution
![[*]](crossref.png) ) and (
) and (![[*]](crossref.png) ), the skewness is,
compared to the kurtosis, a large quantity. Quadratic terms in skewness
could give an equally important contribution to the PDF of
), the skewness is,
compared to the kurtosis, a large quantity. Quadratic terms in skewness
could give an equally important contribution to the PDF of ![[*]](crossref.png) ) interesting consequences for the distribution of
maximum wave heights may be derived. In the narrow band approximation
wave height
) interesting consequences for the distribution of
maximum wave heights may be derived. In the narrow band approximation
wave height ![]() equals
equals ![]() and hence the wave height PDF becomes
and hence the wave height PDF becomes
![[*]](crossref.png) ) from
) from