

Next: Initial Conditions
Up: Numerical Method
Previous: Numerical Method
Two types of nonlinear equations for gravity waves are numerically solved in this study.
One is high-order nonlinear equations which can take into the consideration of the fully nonlinear interactions more than third-order (Dommermuth and Yue, 1987) and another one is the second-order approximated equations which excluded 3rd order nonlinear terms (Yasuda et al., 1992).
It is assumed a periodic boundary condition and is assigned to spatial coordinates  ; the origin is located at the mean water level,
; the origin is located at the mean water level,  the horizontal axis and
the horizontal axis and  the upward vertical axis.
Kinematic and Dynamic boundary conditions on the free surface are rewritten into the evolution equations as a function of the free surface profile
the upward vertical axis.
Kinematic and Dynamic boundary conditions on the free surface are rewritten into the evolution equations as a function of the free surface profile  and the velocity potential on the surface
and the velocity potential on the surface  =
=
 (Zakharov, 1968);
(Zakharov, 1968);
| |
|
 |
(1) |
| |
|
 |
(2) |
where  =
=
 , the subscript
, the subscript  denotes the partial differentiation with
denotes the partial differentiation with  ,
,  the vertical gradient of the velocity potential
the vertical gradient of the velocity potential  ,
,  the time and
the time and  the acceleration due to the gravity.
Dommermuth and Yue (1987) directly solved eqs.(1) and (2) for quasi-monochromatic waves by using a pseudo-spectral method.
They considered an approximation
the acceleration due to the gravity.
Dommermuth and Yue (1987) directly solved eqs.(1) and (2) for quasi-monochromatic waves by using a pseudo-spectral method.
They considered an approximation  up to the order
up to the order  in relative wave steepness.
To skip the detail of the formulation, finally, it is formulated the vertical gradient of velocity potential on the surface as
in relative wave steepness.
To skip the detail of the formulation, finally, it is formulated the vertical gradient of velocity potential on the surface as
 |
(3) |
where  is the order of nonlinearity.
As a result, it can be solved the eqs.(1) and (2) with the approximated
is the order of nonlinearity.
As a result, it can be solved the eqs.(1) and (2) with the approximated  in the Fourier space by using pseudo-spectral method.
The spatial derivations of
in the Fourier space by using pseudo-spectral method.
The spatial derivations of
 and
and  are evaluated in the Fourier space, the nonlinear products are calculated on the physical space.
Therefore, this approach is useful to simulate the long time evolution of random waves having broad band spectra because it requires the CPU time as order of
are evaluated in the Fourier space, the nonlinear products are calculated on the physical space.
Therefore, this approach is useful to simulate the long time evolution of random waves having broad band spectra because it requires the CPU time as order of  , although the mode-coupling equation consumes the CPU time as order of
, although the mode-coupling equation consumes the CPU time as order of  .
All aliasing errors generated in the nonlinear terms are deleted.
The time integration of the Fourier modes of
.
All aliasing errors generated in the nonlinear terms are deleted.
The time integration of the Fourier modes of  and
and
 is evaluated in the Fourier space with the fourth-order Runge-Kutta-Gill method.
The order of nonlinearity
is evaluated in the Fourier space with the fourth-order Runge-Kutta-Gill method.
The order of nonlinearity  was fixed four for all cases that is the fourth-order nonlinear interactions were took into consideration for the high-order nonlinear simulation.
was fixed four for all cases that is the fourth-order nonlinear interactions were took into consideration for the high-order nonlinear simulation.
The accuracy and convergence of the numerical model are verified by propagating the exact solution of the Stoke wave.
The maximum error of the total energy leak and the surface profile change were
 and
and
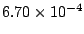 , respectively.
It is hence expect the high-order nonlinear wave propagation with the sufficient accuracy solving eqs.(1), (2) and (3).
, respectively.
It is hence expect the high-order nonlinear wave propagation with the sufficient accuracy solving eqs.(1), (2) and (3).
Figure 1:
Initial profile of wavenumber spectra for 2D simulations given by the Wallops type spectra as a function of spectrum bandwidth 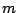 .
.
 |


Next: Initial Conditions
Up: Numerical Method
Previous: Numerical Method
2005-11-21
![]() ; the origin is located at the mean water level,
; the origin is located at the mean water level, ![]() the horizontal axis and
the horizontal axis and ![]() the upward vertical axis.
Kinematic and Dynamic boundary conditions on the free surface are rewritten into the evolution equations as a function of the free surface profile
the upward vertical axis.
Kinematic and Dynamic boundary conditions on the free surface are rewritten into the evolution equations as a function of the free surface profile ![]() and the velocity potential on the surface
and the velocity potential on the surface ![]() =
=
![]() (Zakharov, 1968);
(Zakharov, 1968);
![]() and
and
![]() , respectively.
It is hence expect the high-order nonlinear wave propagation with the sufficient accuracy solving eqs.(1), (2) and (3).
, respectively.
It is hence expect the high-order nonlinear wave propagation with the sufficient accuracy solving eqs.(1), (2) and (3).
