

Next: Numerical Results and Discussions
Up: Numerical Method
Previous: Governing Equations
The amplitudes of initial waves were given by the Wallops type spectrum in wavenumber space transformed through the linear dispersion relation.
![\begin{displaymath}
S(k)\, dk=\frac{\alpha}{2} H_{1/3}^2\kappa^{-{m\over2}}
\ex...
...th} k_ph}}
\left[1+\frac{2kh}{{\rm sh} 2kh}
\right]
\, dk
\end{displaymath}](img34.png) |
(4) |
 |
(5) |
where, 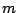 the spectral bandwidth parameter,
the spectral bandwidth parameter, 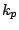 the peak wavenumber of spectra,
the peak wavenumber of spectra,  the water depth and
the water depth and  is a constant satisfying a following relation with
is a constant satisfying a following relation with  :
:
 |
(6) |
Eq.(4) with 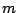 =5 and
=5 and 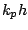 =
=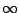 is equivalent to JONSWAP spectra and the shape of spectrum is getting narrower as increasing the value of
is equivalent to JONSWAP spectra and the shape of spectrum is getting narrower as increasing the value of 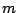 .
The Wallops spectrum is evaluated as a function of spectrum bandwidth
.
The Wallops spectrum is evaluated as a function of spectrum bandwidth 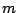 only.
The phase constants of the initial waves were assumed a random phase approximation.
This assumption is very important for simulating realistic random waves.
A further important point is that if the phase is given factitiously(e.g. frequency wave focusing), it is possible to generate a freak wave like surface profile at an arbitrary time and location.
However, such approach is out side of the scope of this study.
only.
The phase constants of the initial waves were assumed a random phase approximation.
This assumption is very important for simulating realistic random waves.
A further important point is that if the phase is given factitiously(e.g. frequency wave focusing), it is possible to generate a freak wave like surface profile at an arbitrary time and location.
However, such approach is out side of the scope of this study.
The computations were made in the periodic space having the length of  . Initial wave statistics were comprised with fixed characteristic wave steepness:
. Initial wave statistics were comprised with fixed characteristic wave steepness: 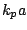 =0.14 and spectrum band width:
=0.14 and spectrum band width: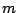 =10, 20, 30, 40, 60, 80 and 100 as shown in Figure 1.
Here,
=10, 20, 30, 40, 60, 80 and 100 as shown in Figure 1.
Here,  is a half of
is a half of  , and
, and  and
and 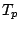 are the wave length and wave period of spectral peak mode, respectively.
The water depth was chosen as
are the wave length and wave period of spectral peak mode, respectively.
The water depth was chosen as 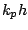 =
=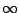 (deep-water), 3.0, 2.0, 1.36, 1.0.
The total time integration was calculated up to
(deep-water), 3.0, 2.0, 1.36, 1.0.
The total time integration was calculated up to  =
= .
.
Figure 2:
Temporal evolutions of the Fourier spectra of the simulated wave train which has steepness 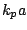 =0.14 and spectrum bandwidth
=0.14 and spectrum bandwidth 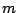 =10, initially.
=10, initially.
 |


Next: Numerical Results and Discussions
Up: Numerical Method
Previous: Governing Equations
2005-11-21
![\begin{displaymath}
S(k)\, dk=\frac{\alpha}{2} H_{1/3}^2\kappa^{-{m\over2}}
\ex...
...th} k_ph}}
\left[1+\frac{2kh}{{\rm sh} 2kh}
\right]
\, dk
\end{displaymath}](img34.png)
![]() . Initial wave statistics were comprised with fixed characteristic wave steepness:
. Initial wave statistics were comprised with fixed characteristic wave steepness: ![]() =0.14 and spectrum band width:
=0.14 and spectrum band width:![]() =10, 20, 30, 40, 60, 80 and 100 as shown in Figure 1.
Here,
=10, 20, 30, 40, 60, 80 and 100 as shown in Figure 1.
Here, ![]() is a half of
is a half of ![]() , and
, and ![]() and
and ![]() are the wave length and wave period of spectral peak mode, respectively.
The water depth was chosen as
are the wave length and wave period of spectral peak mode, respectively.
The water depth was chosen as ![]() =
=![]() (deep-water), 3.0, 2.0, 1.36, 1.0.
The total time integration was calculated up to
(deep-water), 3.0, 2.0, 1.36, 1.0.
The total time integration was calculated up to ![]() =
=![]() .
.
