

Next: Wave Height Distributions
Up: Mathematical formulations
Previous: Mathematical formulations
We assume that waves to be analyzed here are unidirectional with narrow banded spectra and satisfy the stationary and ergodic hypothesis.
Let 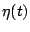 be the sea surface elevation as a function of
be the sea surface elevation as a function of 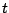 and
and 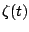 be its Hilbert transform.
Assuming both
be its Hilbert transform.
Assuming both 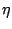 and
and 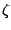 are real zero-mean function with variance
are real zero-mean function with variance 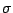 , we have
, we have
The characteristic function 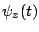 can be described as
can be described as
![\begin{displaymath}
\psi_z(u,v) = E\left[e^{i(u\eta+v\zeta)}\right],
\end{displaymath}](img17.png) |
(4) |
where ![$E[\cdot]$](img18.png) means the expected value operator, and
means the expected value operator, and 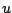 and
and 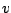 are dummy variables in
are dummy variables in
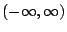 .
.
The cumulants 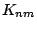 is formulated by Eq.(4) as
is formulated by Eq.(4) as
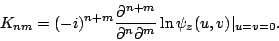 |
(5) |
The following relationship is established between the characteristic function 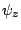 and cumulant
and cumulant 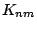 .
between them, so we have
.
between them, so we have
![\begin{displaymath}
\psi_z(u,v) = \exp\left[
\sum_{n}\sum_{m} \frac{K_{nm}}{n!m!}
(iu)^n(iv)^m
\right].
\end{displaymath}](img25.png) |
(6) |
Longuet-Higgins (1963) formulated the detailed relationship between Eq.(5) and Eq.(6).
Several values of cumulants 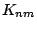 are derived from Eq.(5) on the basic assumptions, stationariness and orthogonal property of
are derived from Eq.(5) on the basic assumptions, stationariness and orthogonal property of 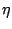 and
and 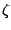 .
.
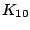 |
 |
![$\displaystyle E[\eta ] = \bar{\eta } = 0$](img27.png) |
(7) |
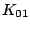 |
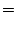 |
![$\displaystyle E[\zeta] = \bar{\zeta} = 0$](img29.png) |
(8) |
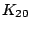 |
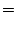 |
![$\displaystyle E[\eta^2] = \eta_{rms}^2$](img31.png) |
(9) |
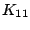 |
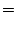 |
![$\displaystyle E[\eta\zeta] = 0$](img33.png) |
(10) |
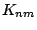 |
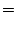 |
![$\displaystyle E[\eta^n\zeta^m]$](img35.png) |
|
| |
|
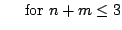 |
(11) |
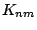 |
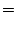 |
![$\displaystyle E[\eta^n\zeta^m] + (n-1)(m-1)(-1)^{n/2}\sigma^{n+m}$](img37.png) |
|
| |
|
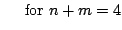 |
(12) |
Similar results can be extended for the higher order cumulants, but the analysis is not carried out here beyond the fourth order.
Mori and Yasuda (1994) pointed out that the fourth order moment of water surface elevation is a dominative parameter for wave height statistics.
In present case, therefore, we should take into consideration up to the fourth order cumulants.
The joint probability density function of 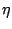 and
and 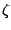 is formulated as
is formulated as
where
and 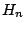 is the
is the 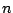 th order Hermite polynomial expressed as
th order Hermite polynomial expressed as
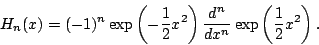 |
(17) |
It is noticed here that 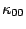 =
=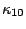 =
=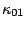 =
=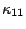 =0,
=0, 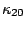 =
= 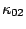 =1 and
=1 and 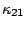 =
=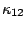 =
=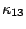 =
=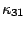 =0, which have already been used in Eq.(7).
=0, which have already been used in Eq.(7).
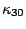 is equal to the skewness
is equal to the skewness 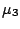 of
of 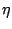 and
and 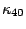 is equal to kurtosis
is equal to kurtosis 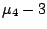 .
There is still unknown cumulants such as
.
There is still unknown cumulants such as 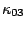 ,
, 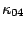 ,
, 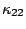 .
.
Tayfun (1993) formulated 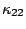 for weakly nonlinear waves wtih narrow banded spectra using the second order kernel function in deep water as,
for weakly nonlinear waves wtih narrow banded spectra using the second order kernel function in deep water as,
where 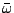 is the mean angular frequency of spectrum and
is the mean angular frequency of spectrum and 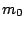 is sum of spectrum of the first order component.
is sum of spectrum of the first order component.
By way of Schwarz's inequality an equality,
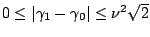 is derived.
This gives
is derived.
This gives
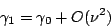 |
(20) |
and
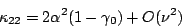 |
(21) |
Since, the maximum value of 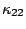 is
is 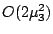 , it is assumed there that
, it is assumed there that 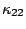 =0 and also
=0 and also 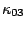 =
= 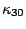 and
and 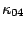 =
= 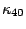 under the condition of weak nonlinearlity.
under the condition of weak nonlinearlity.


Next: Wave Height Distributions
Up: Mathematical formulations
Previous: Mathematical formulations
2005-11-21
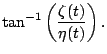
![]() is formulated by Eq.(4) as
is formulated by Eq.(4) as
![]() are derived from Eq.(5) on the basic assumptions, stationariness and orthogonal property of
are derived from Eq.(5) on the basic assumptions, stationariness and orthogonal property of ![]() and
and ![]() .
.
![]() and
and ![]() is formulated as
is formulated as
![]() for weakly nonlinear waves wtih narrow banded spectra using the second order kernel function in deep water as,
for weakly nonlinear waves wtih narrow banded spectra using the second order kernel function in deep water as,
![]() is derived.
This gives
is derived.
This gives
![]() is
is ![]() , it is assumed there that
, it is assumed there that ![]() =0 and also
=0 and also ![]() =
= ![]() and
and ![]() =
= ![]() under the condition of weak nonlinearlity.
under the condition of weak nonlinearlity.