


Next: Conclusions
Up: AIR-BUBBLE MEASUREMENTS OF THE
Previous: Method of Visualization
A flat LED light (10cm 10cm) was used for the shadow graph to avoid flicker of the back light.
A continuous diode laser operated at a power of 5W and a wavelength of 532 nm was used as the light source to adjust the exact location of bubble in transverse direction of bubble between the camera and the back light.
A cylindrical lens mounted in front of the laser was used to create the light sheet.
An 8-bit high speed CMOS camera with a resolution of 1280
10cm) was used for the shadow graph to avoid flicker of the back light.
A continuous diode laser operated at a power of 5W and a wavelength of 532 nm was used as the light source to adjust the exact location of bubble in transverse direction of bubble between the camera and the back light.
A cylindrical lens mounted in front of the laser was used to create the light sheet.
An 8-bit high speed CMOS camera with a resolution of 1280 1024 pixels was used to capture the images.
The images were captured at a framing rate of 125-250 frames per second.
Each captured image was stored in a PC and later analyzed using the BTV image processing technique with results similar to those shown in Fig.
1024 pixels was used to capture the images.
The images were captured at a framing rate of 125-250 frames per second.
Each captured image was stored in a PC and later analyzed using the BTV image processing technique with results similar to those shown in Fig.![[*]](crossref.png) .
The uncertainty owing to image distortion was also checked using fixed markers in the tank and found that the maximum error was 1.5 mm (about 5 pixels).
Fig.
.
The uncertainty owing to image distortion was also checked using fixed markers in the tank and found that the maximum error was 1.5 mm (about 5 pixels).
Fig.![[*]](crossref.png) shows the sample of BTV experimental setup using two cameras.
The half mirror was used to divide one image into two cameras.
The two cameras can be installed different lens to enhance the
resolution of field of view (FOV).
However, only one camera was used in this study.
shows the sample of BTV experimental setup using two cameras.
The half mirror was used to divide one image into two cameras.
The two cameras can be installed different lens to enhance the
resolution of field of view (FOV).
However, only one camera was used in this study.
Figure:
Illustration of experimental setup
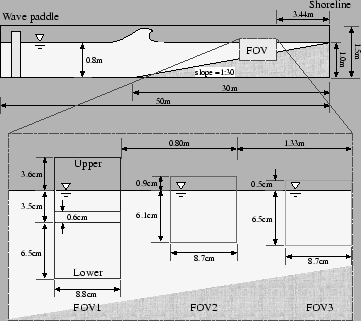 |
The breaking wave experiments were conducted in a wave tank that is 50.0 m long, 1.0 m wide, and 1.5 m deep located in Osaka City University.
The one side wall of the tank was constructed using glass for optical access.
The BTV imaging system shown in Fig.![[*]](crossref.png) was set up in the middle of the tank.
A fixed, impermeable 1/30 slope was installed with the toe 20 from the wavemaker.
The water depth was 1.0 m, and regular wave trains were generated by
a computer-controlled piston-type wavemaker with active absorber
A detail of the experimental setup is shown in Fig.
was set up in the middle of the tank.
A fixed, impermeable 1/30 slope was installed with the toe 20 from the wavemaker.
The water depth was 1.0 m, and regular wave trains were generated by
a computer-controlled piston-type wavemaker with active absorber
A detail of the experimental setup is shown in Fig.![[*]](crossref.png)
Figure:
Time history of void fraction (solid line: void fraction,
dashed line: area of liquid in the image)
 |
The three different locations were chosen as field of view (FOV) of the
BTV measurements.
The FOV 1-3 were located at 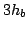 ,
, 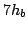 and
and 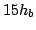 , respectively.
Here
, respectively.
Here 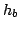 denotes the water depth at the breaking point (B.P.).
The void fraction in this study is defined by the spatial ratio to bulk
of air and water below the free surface.
Therefore, the location of the free surface becomes important to define
the void fraction.
The edge detection method as same as bubble shape detection was used to
identify the free surface.
The threshold value of edge detection for the free surface was selected
through the trial and error through the checking process.
denotes the water depth at the breaking point (B.P.).
The void fraction in this study is defined by the spatial ratio to bulk
of air and water below the free surface.
Therefore, the location of the free surface becomes important to define
the void fraction.
The edge detection method as same as bubble shape detection was used to
identify the free surface.
The threshold value of edge detection for the free surface was selected
through the trial and error through the checking process.
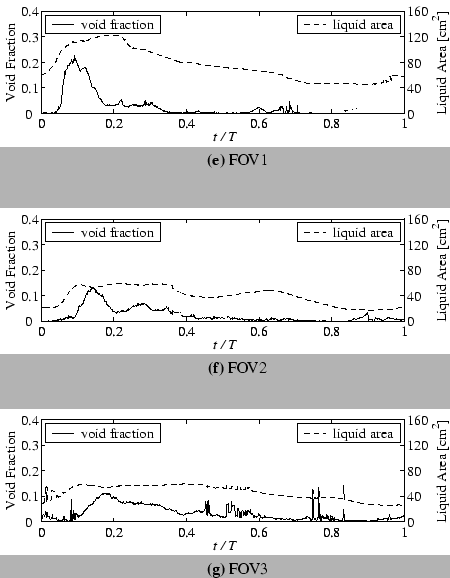
Fig.![[*]](crossref.png) shows an example of the instantaneous time series of void
fraction measured by the BTV.
The solid and dashed line denote void fraction, and area of liquid in the
image.
The spatial-averaged void fractions do not decreased monotonically as
() investigated.
This is because the difference between the instantaneous (BTV measured) and
phase-averaged void fraction (void fraction measured).
The measured time series of void fraction have several interesting
characteristics, although measurement locations were limited to discuss
in detail.
First, the maximum values of void fraction were decreased as breaking
wave propagates to shoreline (FOV1
shows an example of the instantaneous time series of void
fraction measured by the BTV.
The solid and dashed line denote void fraction, and area of liquid in the
image.
The spatial-averaged void fractions do not decreased monotonically as
() investigated.
This is because the difference between the instantaneous (BTV measured) and
phase-averaged void fraction (void fraction measured).
The measured time series of void fraction have several interesting
characteristics, although measurement locations were limited to discuss
in detail.
First, the maximum values of void fraction were decreased as breaking
wave propagates to shoreline (FOV1
 FOV3).
The void fraction at FOV1 (
FOV3).
The void fraction at FOV1 (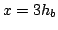 ) exceeds 0.2 but is about 0.1 at
FOV3 (
) exceeds 0.2 but is about 0.1 at
FOV3 (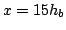 ).
Second, the rising up of void fraction from 0 to the maximum at FOV1 is faster
than the others and is decreased as FOV1
).
Second, the rising up of void fraction from 0 to the maximum at FOV1 is faster
than the others and is decreased as FOV1
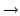 FOV3.
In addition, the decreasing rates of void fraction after reached maximum
value show the similar tendency.
Thus, the bulk of air was massively injected into the water near the
B.P. and was diffused as wave propagated to shoreline.
The BTV can be measured these characteristics from the spatial-averaged
(depth-averaged) point of view.
FOV3.
In addition, the decreasing rates of void fraction after reached maximum
value show the similar tendency.
Thus, the bulk of air was massively injected into the water near the
B.P. and was diffused as wave propagated to shoreline.
The BTV can be measured these characteristics from the spatial-averaged
(depth-averaged) point of view.
Figure:
Time series of bubble size distribution
 |
Fig.![[*]](crossref.png) shows the time series of bubble diameter distribution.
The bubble diameter denotes mean value of major and minor diameter of elliptic
approximation of 2D projected plane.
The horizontal axes are time normalized by the incident wave period and
the characteristics diameter.
The vertical axis is number of bubbles per unit area.
The bubble number density usually has a dimension of [Number of
bubbles/
m
shows the time series of bubble diameter distribution.
The bubble diameter denotes mean value of major and minor diameter of elliptic
approximation of 2D projected plane.
The horizontal axes are time normalized by the incident wave period and
the characteristics diameter.
The vertical axis is number of bubbles per unit area.
The bubble number density usually has a dimension of [Number of
bubbles/
m ] but the BTV is 2D measurement therefore the
bubble number density is normalized by unit area.
As already shown in Fig.
] but the BTV is 2D measurement therefore the
bubble number density is normalized by unit area.
As already shown in Fig.![[*]](crossref.png) , the bulk of air injected into the free
surface rapidly and decreased near the breaking point (FOV1) rather than far field (FOV3).
The time series of the bubble number density distribution, Fig.
, the bulk of air injected into the free
surface rapidly and decreased near the breaking point (FOV1) rather than far field (FOV3).
The time series of the bubble number density distribution, Fig.![[*]](crossref.png) , shows
similar tendency but the number of small scale bubble has different behavior.
Generally, entrapped air by breaking waves is split into small bubbles owing to
the shear and turbulence of surrounding flows.
The early work of this problem for a general condition discussed by
() and () in the middle of the last
century and a large bibliography has been generated (i.e. , ).
The bubble size spectra in FOV1 and 3 show two clear peaks, but the
appeared time of peaks is different as shown in Fig.
, shows
similar tendency but the number of small scale bubble has different behavior.
Generally, entrapped air by breaking waves is split into small bubbles owing to
the shear and turbulence of surrounding flows.
The early work of this problem for a general condition discussed by
() and () in the middle of the last
century and a large bibliography has been generated (i.e. , ).
The bubble size spectra in FOV1 and 3 show two clear peaks, but the
appeared time of peaks is different as shown in Fig.![[*]](crossref.png) (a) and (c).
The number of small size bubble smaller than 1mm increased significantly.
The difference of the bubble size spectra between FOV1 and 3 can be
explained by the bubble splitting owing to strong shear flow generated
by the breaking waves.
The detail of small scale bubble characteristics related with the power-law scaling of bubble size spectra is discussed next.
(a) and (c).
The number of small size bubble smaller than 1mm increased significantly.
The difference of the bubble size spectra between FOV1 and 3 can be
explained by the bubble splitting owing to strong shear flow generated
by the breaking waves.
The detail of small scale bubble characteristics related with the power-law scaling of bubble size spectra is discussed next.
Figure:
Power law of bubble size distribution
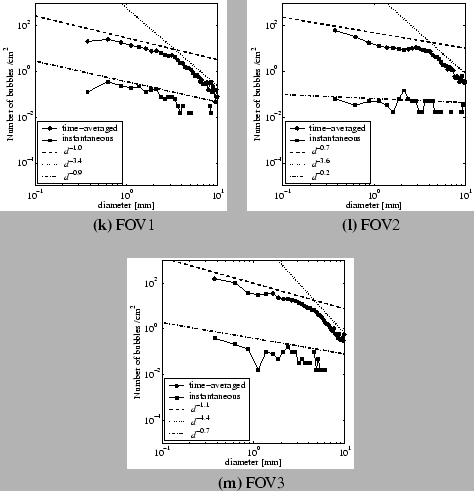 |
To check the power-law scaling of the bubble size spectra in the surf zone,
Fig.![[*]](crossref.png) shows the instantaneous and time-averaged bubble size spectra
with the estimated power-law by the least-square method.
The instantaneous bubble size spectra corresponds at the time of the
maximum void fraction.
There are two scaling laws can be seen at all FOVs.
The small and large size bubble power scaling laws are
shows the instantaneous and time-averaged bubble size spectra
with the estimated power-law by the least-square method.
The instantaneous bubble size spectra corresponds at the time of the
maximum void fraction.
There are two scaling laws can be seen at all FOVs.
The small and large size bubble power scaling laws are
 and
and
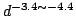 , respectively.
There is no significant difference between instantaneous and
time-averaged spectra.
The critical point in between two power scaling corresponds to the Hinze
scale of bubble splitting theory (, ).
() proposed semi-empirical
, respectively.
There is no significant difference between instantaneous and
time-averaged spectra.
The critical point in between two power scaling corresponds to the Hinze
scale of bubble splitting theory (, ).
() proposed semi-empirical  power-law scaling for
the bubble which is larger than the Hinze scale based on the
discussion of bubble fragmentation in the strong turbulence flow below the trough level.
The measured power-law scaling of large size bubble size spectra is
similar to ().
On the other hand, () measured a
power-law scaling for
the bubble which is larger than the Hinze scale based on the
discussion of bubble fragmentation in the strong turbulence flow below the trough level.
The measured power-law scaling of large size bubble size spectra is
similar to ().
On the other hand, () measured a 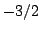 power-law
scaling, smaller than the Hinze scale (1mm) of the acoustically active
phase near the crest.
The power-law scaling of small size bubble shown in
Fig.
power-law
scaling, smaller than the Hinze scale (1mm) of the acoustically active
phase near the crest.
The power-law scaling of small size bubble shown in
Fig.![[*]](crossref.png) is close to
is close to 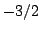 power-law predicted by ().
The Hinze scale of time-averaged spectra at FOV1 is smaller than FOV3.
This is related with the turbulent intensity and energy dissipation
induced by the breaking waves.
The detail mechanisms and relationship between the Hinze scale and
energy dissipation require liquid phase measurements and should keep for future study.
power-law predicted by ().
The Hinze scale of time-averaged spectra at FOV1 is smaller than FOV3.
This is related with the turbulent intensity and energy dissipation
induced by the breaking waves.
The detail mechanisms and relationship between the Hinze scale and
energy dissipation require liquid phase measurements and should keep for future study.



Next: Conclusions
Up: AIR-BUBBLE MEASUREMENTS OF THE
Previous: Method of Visualization
2007-02-21
![[*]](crossref.png) .
The uncertainty owing to image distortion was also checked using fixed markers in the tank and found that the maximum error was 1.5 mm (about 5 pixels).
Fig.
.
The uncertainty owing to image distortion was also checked using fixed markers in the tank and found that the maximum error was 1.5 mm (about 5 pixels).
Fig.![[*]](crossref.png) shows the sample of BTV experimental setup using two cameras.
The half mirror was used to divide one image into two cameras.
The two cameras can be installed different lens to enhance the
resolution of field of view (FOV).
However, only one camera was used in this study.
shows the sample of BTV experimental setup using two cameras.
The half mirror was used to divide one image into two cameras.
The two cameras can be installed different lens to enhance the
resolution of field of view (FOV).
However, only one camera was used in this study.



