

Next: Surface wave profile and
Up: Numerical Results and Discussions
Previous: Numerical Results and Discussions
Figure 2 shows the time evolutions of the wavenumber spectra for 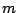 =10 and
=10 and 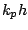 =
=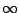 both of the high-order and the second-order solution.
Although both simulations were started with the same initial condition, there is a significant difference of the spectrum evolution between them.
It is found that the Fourier modes actively exchange their energy and the Fourier mode amplitudes are strongly modulated during the propagation process for the high-order solution, while the second-order solution seems to stable.
The fact that the differences between the high-order solution and the second-order one in Figure 2 suggest that the Fourier modes can transfer the energy due to the high-order nonlinear interactions even if the spectrum band width is relatively broad.
A similar relation was observed in various spectrum band width in deep-water condition, however the activity of energy transfer became weak if initial spectrum band width became broader.
The amplitude modulation like behavior became weak as deceasing the water depth and it finally disappeared if the characteristic water depth
both of the high-order and the second-order solution.
Although both simulations were started with the same initial condition, there is a significant difference of the spectrum evolution between them.
It is found that the Fourier modes actively exchange their energy and the Fourier mode amplitudes are strongly modulated during the propagation process for the high-order solution, while the second-order solution seems to stable.
The fact that the differences between the high-order solution and the second-order one in Figure 2 suggest that the Fourier modes can transfer the energy due to the high-order nonlinear interactions even if the spectrum band width is relatively broad.
A similar relation was observed in various spectrum band width in deep-water condition, however the activity of energy transfer became weak if initial spectrum band width became broader.
The amplitude modulation like behavior became weak as deceasing the water depth and it finally disappeared if the characteristic water depth 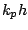 was shallower than 1.36.
was shallower than 1.36.
Figure 3:
The time-averaged the spectra over 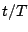 =30 to 100 and their relations to the initial bandwidth
=30 to 100 and their relations to the initial bandwidth 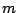 .
.
|
Figure 3 shows the time averaged wavenumber spectra both the high-order and second-order solution in deep-water condition.
The second-order solution shows a secondary peak in the higher harmonics, if initial spectrum band width is narrow.
On the contrary, there is no significant differences among the time averaged wavenumber spectra of the high-order solution.
This result demonstrate that spectra of random wave trains in deep-water transform their profiles through the high-order nonlinear resonant interaction and it is equivalent to phase averaged high-order equation(e.g. Hasselmann's eq.)
It appears that the shapes of time averaged spectra of the high-order solution are similar and independent from the initial spectrum band width.
However, effects of the initial spectrum band width are hidden from the shape of the time averaged spectra but are found in dispersion relations.
The phase of the nonlinear wave is given by
 |
(7) |
where  the phase constant,
the phase constant,  the angular frequency as a function of
the angular frequency as a function of  and
and  .
Then the nonlinear dispersion relation
.
Then the nonlinear dispersion relation  =
= can be calculated numerically from the finite differentiation of the phase
can be calculated numerically from the finite differentiation of the phase  :
:
 |
(8) |
Figure 4:
Relationship between the relative phase speed 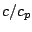 and the relative wavenumber
and the relative wavenumber 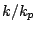 of the high-order and linear solutions.
of the high-order and linear solutions.
 |
Figure 4 shows the relationship between the phase speed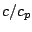 and the wavenumber
and the wavenumber  of the high-order nonlinear solution for
of the high-order nonlinear solution for 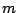 =10 and
=10 and 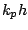 =
=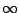 .
The solid line in the figure denotes the nonlinear dispersion relation calculated by Eqn.(8), the dashed line denotes the linear dispersion relation, the dashed line with filled circles and the solid line with filled triangle denote wavenumber spectra at
.
The solid line in the figure denotes the nonlinear dispersion relation calculated by Eqn.(8), the dashed line denotes the linear dispersion relation, the dashed line with filled circles and the solid line with filled triangle denote wavenumber spectra at 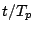 =0 and 100, respectively.
The nonlinear dispersion relation is separated from the linear dispersion relation at the high wavenumber
=0 and 100, respectively.
The nonlinear dispersion relation is separated from the linear dispersion relation at the high wavenumber  .
The points to separate from the linear dispersion relation were depended on the initial spectrum band width and were shifted to low wave number side for the initially narrow banded spectrum case.
The fact that a nonlinear wave grouping become dominant for narrow banded spectrum wave suggests that the nonlinear components of the spectrum is important to describe the nonlinear characteristic of the wave train.
.
The points to separate from the linear dispersion relation were depended on the initial spectrum band width and were shifted to low wave number side for the initially narrow banded spectrum case.
The fact that a nonlinear wave grouping become dominant for narrow banded spectrum wave suggests that the nonlinear components of the spectrum is important to describe the nonlinear characteristic of the wave train.
Figure 5:
Examples of simulated water surface profiles both of the high-order and the second-order solution at the time 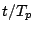 =25.
=25.
 |


Next: Surface wave profile and
Up: Numerical Results and Discussions
Previous: Numerical Results and Discussions
2005-11-21

 of the high-order nonlinear solution for
of the high-order nonlinear solution for